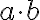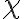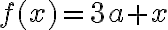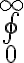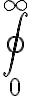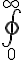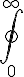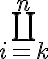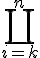Browse the glossary using this index
Special |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
ALL
cdot (multiplication) $$a\cdot~b$$ gives 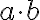 |
|
chi (lower case greek letter) $$\chi$$ gives 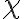 |
|
constants - Numbers in formulas are interpreted as constants and they are rendered in non-italic roman font face, which is a widely used convention.
- Following this convention, variables are shown in italic.
- Exp.: $$f(x)=3a+x$$ gives
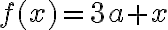
|
|
contour integral - General syntax for symbols with a kind of lower and upper limits:
\symbolname_{lowerexpression}^{upperexpression} - In general, there are two ways how these lower and upper expressions can be placed: centered below and above the symbol or in a subscript / superscript manner. In the first case the symbol name is preceded by the word "big", in the second there is no prefix.
- Syntax for the contour integral symbol:
$$\bigoint_{0}^{\infty}$$ gives 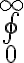
and $$\oint_{0}^{\infty}$$ gives 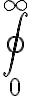
$$\LARGE\bigoint_{\small0}^{\small\infty}$$ gives 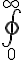
and $$\large\oint_{\small0}^{\small\infty}$$ gives 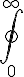
|
|
coproduct - General syntax for symbols with a kind of lower and upper limits:
\symbolname_{lowerexpression}^{upperexpression} - In general, there are two ways how these lower and upper expressions can be placed: centered below and above the symbol or in a subscript / superscript manner. In the first case the symbol name is preceded by the word "big", in the second there is no prefix.
- Note: mimeTeX seems currently only to support the \bigcoprod command.
- Syntax for coproduct symbol:
$$\bigcoprod_{i=k}^{n}$$ gives 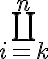
$$\LARGE\bigcoprod_{\small{i=k}}^{\small~n}$$ gives 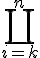
|
|